Laplace Transform¶
Laplace transform of 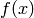 is:
is:
![L[f(x)] = \int_0^{\infty} f(x) e^{-s x}\,\d x
L^{-1}[\bar f(s)]
= {1\over2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty}
\bar f(s) e^{s x}\,\d s
= \sum_{s_0} \res_{s=s_0} (\bar f(s) e^{s x})](../../_images/math/8939823ab6133af32f1845a2d1adef453446dcd2.png)
The contour integration is over the vertical line 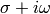 and
and 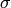 is chosen large enough so that all residues are to the left of the line (that’s
because the Laplace transform
is chosen large enough so that all residues are to the left of the line (that’s
because the Laplace transform 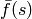 is only defined for
is only defined for  larger than
the residues, so we have to integrate in this range as well). It can be shown
that the integral over the left semicircle goes to zero:
larger than
the residues, so we have to integrate in this range as well). It can be shown
that the integral over the left semicircle goes to zero:
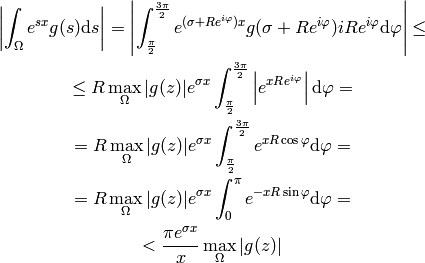
so the complex integral is equal to the sum of all residues of 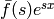 in the complex plane.
in the complex plane.
To show that it works:
![L^{-1} L [f(x)]
=
{1\over2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty}
\left[\int_0^{\infty}
f(x) e^{-s x}\,\d x\right] e^{s x}\,\d s
=
{1\over2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty}
\left[\int_0^{\infty}
f(x') e^{-s x'}\,\d x'\right] e^{s x}\,\d s
=
=
\int_0^{\infty} f(x') \left[{1\over2\pi i}
\int_{\sigma-i\infty}^{\sigma+i\infty}
e^{s (x- x')}\,\d s \right] \,\d x'
=
\int_0^{\infty} f(x') \delta(x-x') \,\d x'
=f(x)](../../_images/math/e35a8957cafe2ab1c2039d94f29c8fd06596c54f.png)
where we used:
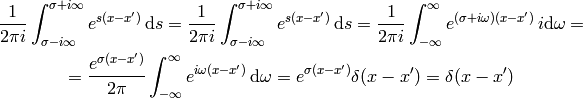
and it can be derived from the Fourier transform by
transforming a function 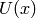 :
:
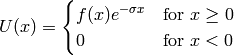
and making a substitution 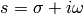 :
:
![L[f(x)] \equiv \bar f(s) = F[U(x)] \equiv \tilde U(\omega)
= \int_{-\infty}^{\infty} U(x) e^{-i\omega x}\,\d x
= \int_0^{\infty} f(x) e^{-\sigma x} e^{-i\omega x}\,\d x
= \int_0^{\infty} f(x) e^{-s x}\,\d x
L^{-1}[\bar f(s)] \equiv f(x) = U(x) e^{\sigma x}
= F^{-1}[\tilde U(\omega)]e^{\sigma x}
= F^{-1}[\bar f(s)]e^{\sigma x}
= F^{-1}[\bar f(\sigma+i\omega)e^{\sigma x}]
= {1\over2\pi}\int_{-\infty}^{\infty} \bar f(\sigma + i\omega)e^{\sigma x}
e^{i\omega x}\,\d \omega
= {1\over2\pi i}\int_{\sigma-i\infty}^{\sigma+i\infty}
\bar f(s) e^{s x}\,\d s
= \sum_{s_0} \res_{s=s_0} (\bar f(s) e^{s x})](../../_images/math/2be27d3ddb29bec572de95bb7e366faad0dc3748.png)
Where the bar (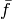 ) means the Laplace transform and tilde (
) means the Laplace transform and tilde (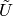 )
means the Fourier transform.
)
means the Fourier transform.
![F[f(x)] \equiv \tilde f(\omega)
= \int_{-\infty}^{\infty} f(x) e^{-i\omega x}\,\d x
F^{-1}[\tilde f(\omega)] = f(x)
= {1\over2\pi}\int_{-\infty}^{\infty}
\tilde f(\omega) e^{+i\omega x}\,\d \omega](../../_images/math/9fb62c3445027a0cb4e744bb622c727f548308f3.png)
![F^{-1} F [f(x)]
=
{1\over2\pi}\int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty}
f(x) e^{-i\omega x}\,\d x\right] e^{+i\omega x}\,\d \omega
=
{1\over2\pi}\int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty}
f(x') e^{-i\omega x'}\,\d x'\right] e^{+i\omega x}\,\d \omega
=
=
\int_{-\infty}^{\infty} f(x') \left[{1\over2\pi}\int_{-\infty}^{\infty}
e^{i\omega (x- x')}\,\d \omega \right] \,\d x'
=
\int_{-\infty}^{\infty} f(x') \delta(x-x') \,\d x'
=f(x)](../../_images/math/a0f1e4fbee5dd57836921191bbe74736bff28d4a.png)