Polar and Spherical Coordinates¶
Polar coordinates (radial, azimuth) 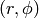 are defined by
are defined by
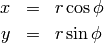
Spherical coordinates (radial, zenith, azimuth) 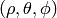 :
:
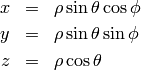
Note: this meaning of 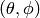 is mostly used in the USA and in many
books. In Europe people usually use different symbols, like
is mostly used in the USA and in many
books. In Europe people usually use different symbols, like 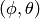 ,
, 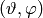 and others.
and others.
Argument function, atan2¶
Argument function 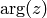 is any
is any 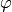 such that
such that
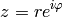
Obviously 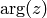 is unique up to any integer multiple of
is unique up to any integer multiple of 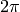 . By taking
the principal value of the
. By taking
the principal value of the 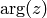 function, e.g. fixing
function, e.g. fixing 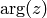 to the
interval
to the
interval ![(-\pi, \pi]](../../_images/math/e520a7aeab7e3c5078aebf7d07340c9485d2a110.png) , we get the
, we get the 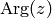 function:
function:
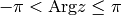
then 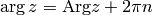 , where
, where 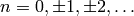 . We can then
use the following formula to easily calculate
. We can then
use the following formula to easily calculate 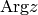 for any
for any 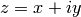 (except
(except
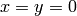 , i.e.
, i.e. 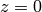 ):
):
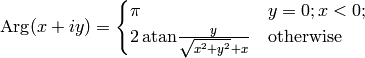
Finally we define 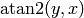 as:
as:
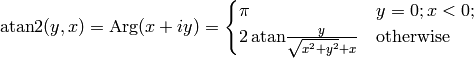
The angle 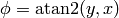 is the angle of the point
is the angle of the point 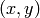 on the unit
circle (assuming the usual conventions), and it works for all quadrants
(
on the unit
circle (assuming the usual conventions), and it works for all quadrants
(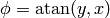 only works for the first and fourth quadrant, where
only works for the first and fourth quadrant, where
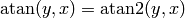 , but in the second and third qudrant,
, but in the second and third qudrant, 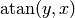 gives the wrong angles, while
gives the wrong angles, while 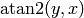 gives the correct angles). So in
particular:
gives the correct angles). So in
particular:
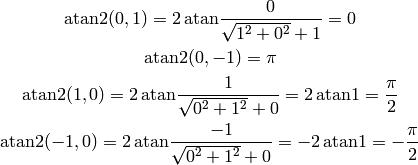
This convention (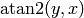 ) is used for example in Python, C or Fortran.
Some people might interchange
) is used for example in Python, C or Fortran.
Some people might interchange 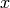 with
with 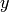 in the definition (i.e.
in the definition (i.e. 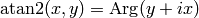 ), but it is not very common.
), but it is not very common.
The following useful relations hold:
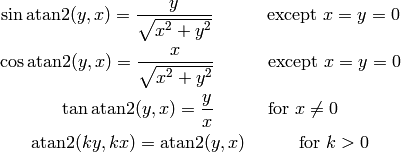
We now prove them. The following works for all  except for
except for  :
:
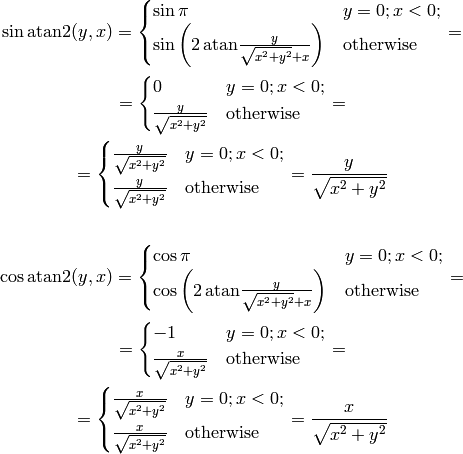
Tangent is infinite for 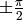 , which corresponds to
, which corresponds to 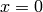 , so the
following works for all
, so the
following works for all 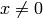 :
:
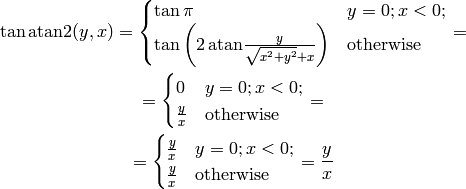
In the above, we used the following double angle formulas:
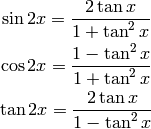
to simplify the following expressions:
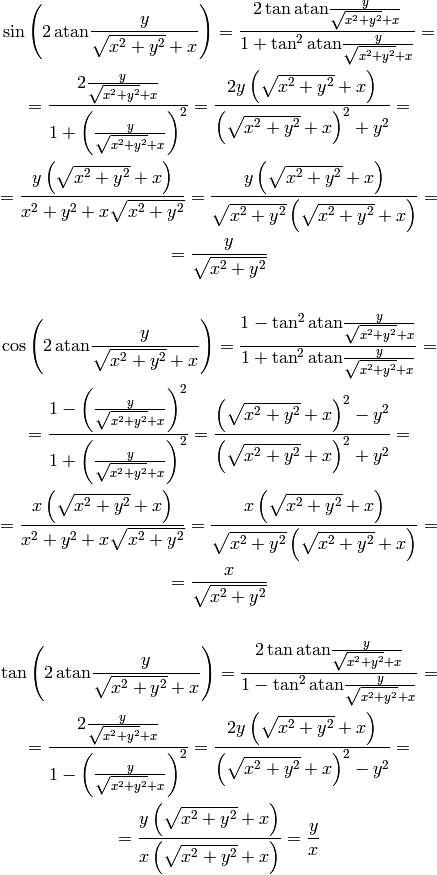
Finally, for all  we get:
we get:
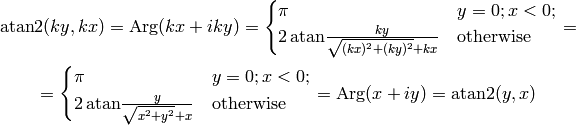
An example of an application:
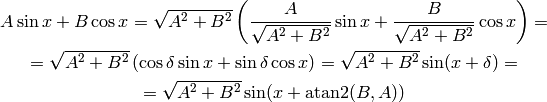
where
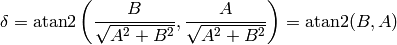
Delta Function¶
Delta function 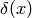 is defined such that this relation holds:
is defined such that this relation holds:
(1)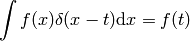
No such function exists, but one can find many sequences “converging” to a delta function:
(2)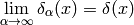
more precisely:
(3)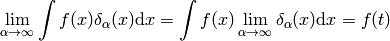
one example of such a sequence is:
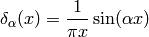
It’s clear that (3) holds for any well behaved function 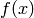 .
Some mathematicians like to say that it’s incorrect to use such a notation when
in fact the integral (1) doesn’t “exist”, but we will not follow
their approach, because it is not important if something “exists” or not,
but rather if it is clear what we mean by our notation: (1) is a
shorthand for (3) and (2) gets a mathematically rigorous
meaning when you integrate both sides and use (1) to arrive at
(3). Thus one uses the relations (1), (2),
(3) to derive all properties of the delta function.
.
Some mathematicians like to say that it’s incorrect to use such a notation when
in fact the integral (1) doesn’t “exist”, but we will not follow
their approach, because it is not important if something “exists” or not,
but rather if it is clear what we mean by our notation: (1) is a
shorthand for (3) and (2) gets a mathematically rigorous
meaning when you integrate both sides and use (1) to arrive at
(3). Thus one uses the relations (1), (2),
(3) to derive all properties of the delta function.
Let’s give an example. Let 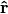 be the unit vector in 3D and we can label it using spherical coordinates
be the unit vector in 3D and we can label it using spherical coordinates 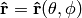 . We can also express it in cartesian coordinates as
. We can also express it in cartesian coordinates as 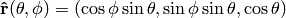 .
.
(4)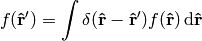
Expressing 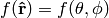 as a function of
as a function of 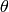 and
and 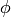 we have
we have
(5)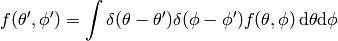
Expressing (4) in spherical coordinates we get
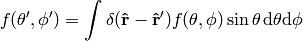
and comparing to (5) we finally get
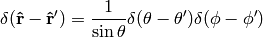
In exactly the same manner we get
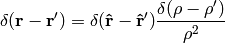
See also (6) for an example of how to deal with more complex expressions involving the delta function like 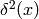 .
.
Distributions¶
Some mathematicians like to use distributions and a mathematical notation for that, which I think is making things less clear, but nevertheless it’s important to understand it too, so the notation is explained in this section, but I discourage to use it – I suggest to only use the physical notation as explained below. The math notation below is put into quotation marks, so that it’s not confused with the physical notation.
The distribution is a functional and each function 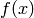 can be identified
with a distribution
can be identified
with a distribution 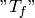 that it generates using this definition (
that it generates using this definition (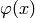 is a test function):
is a test function):
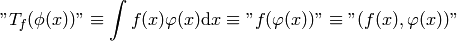
besides that, one can also define distributions that can’t be identified with regular functions, one example is a delta distribution (Dirac delta function):
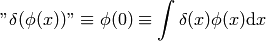
The last integral is not used in mathematics, in physics on the other hand, the
first expressions (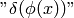 ) is not used, so
) is not used, so 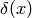 always means
that you have to integrate it, as explained in the previous section, so it
behaves like a regular function (except that such a function doesn’t exist and
the precise mathematical meaning is only after you integrate it, or through the
identification above with distributions).
always means
that you have to integrate it, as explained in the previous section, so it
behaves like a regular function (except that such a function doesn’t exist and
the precise mathematical meaning is only after you integrate it, or through the
identification above with distributions).
One then defines common operations via acting on the generating function, then observes the pattern and defines it for all distributions. For example differentiation:
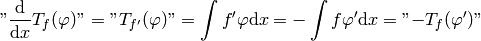
so:
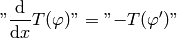
Multiplication:
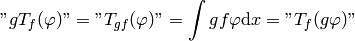
so:
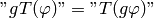
Fourier transform:
![\mathnot{FT_f(\varphi)} =
\mathnot{T_{Ff}(\varphi)} =
\int F(f)\varphi \d x =
=\int\left[\int e^{-ikx} f(k) \d k\right] \varphi(x) \d x
=\int f(k)\left[\int e^{-ikx} \varphi(x) \d x\right] \d k
=\int f(x)\left[\int e^{-ikx} \varphi(k) \d k\right] \d x
=
=
\int f F(\varphi) \d x =
\mathnot{T_f(F\varphi)}](../../_images/math/99ff14da52d12b993ca97412c35f70755ffe200a.png)
so:
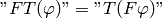
But as you can see, the notation is just making things more complex, since it’s enough to just work with the integrals and forget about the rest. One can then even omit the integrals, with the understanding that they are implicit.
Some more examples:
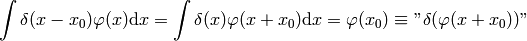
Proof of 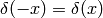 :
:
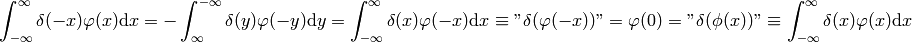
Proof of 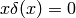 :
:
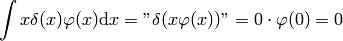
Proof of 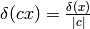 :
:
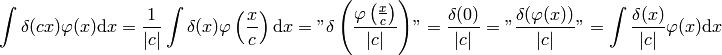
Variations and Functional Derivatives¶
Functional derivatives are a common source of confusion and especially the notation. The reason is similar to the delta function — the definition is operational, i.e. it tells you what operations you need to do to get a mathematically precise formula. The notation below is commonly used in physics and in our opinion it is perfectly precise and exact, but some mathematicians may not like it.
Let’s have  . The function
. The function 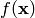 assigns a number to each
assigns a number to each 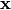 . We define a differential of
. We define a differential of 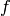 as
as
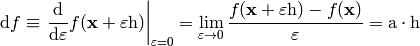
The last equality follows from the fact, that 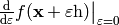 is a linear function of
is a linear function of 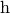 . We define
. We define 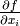 as
as
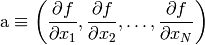
This also gives a formula for computing 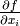 : we set
: we set 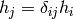 and
and
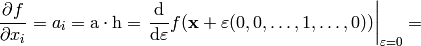
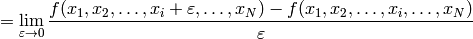
But this is just the way the partial derivative is usually defined. Every variable can be treated as a function (very simple one):
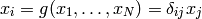
and so we define
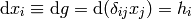
and thus we write 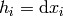 and
and 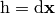 and
and
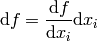
So 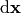 has two meanings — it’s either
has two meanings — it’s either 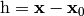 (a finite change in the independent variable
(a finite change in the independent variable 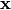 ) or a differential, depending on the context. Even mathematicians use this notation.
) or a differential, depending on the context. Even mathematicians use this notation.
Functional ![F[f]](../../_images/math/d5efc0eec270c88592417add1233cfeaa51564e3.png) assigns a number to each function
assigns a number to each function 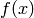 . The variation is defined as
. The variation is defined as
![\delta F[f]\equiv\left.{\d\over\d\varepsilon}F[f+\varepsilon h] \right|_{\varepsilon=0}=\lim_{\epsilon\to0}{F[f+\epsilon h]-F[f]\over\epsilon}= \int a(x)h(x)\d x](../../_images/math/07dd13ee0b73980dd443e90f846d99b53b9b41ea.png)
We define 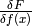 as
as
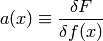
This also gives a formula for computing 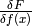 : we set
: we set 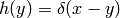 and
and
![{\delta F\over\delta f(x)}=a(x)=\int a(y)\delta(x-y)\d y= \left.{\d\over\d\varepsilon}F[f(y)+\varepsilon\delta(x-y)] \right|_{\varepsilon=0}=](../../_images/math/40341c13ce31d8100306c3056db74b3762a8f1ae.png)
![=\lim_{\varepsilon\to0} {F[f(y)+\varepsilon\delta(x-y)]-F[f(y)]\over\varepsilon}](../../_images/math/0afc916533d2ef2008af1831413045e6a0693131.png)
Every function can be treated as a functional (although a very simple one):
![f(x)=G[f]=\int f(y)\delta(x-y)\d y](../../_images/math/387f075e6d71f2a505dac776f7e17e0c76da8f10.png)
and so we define
![\delta f\equiv\delta G[f]= \left.{\d\over\d\varepsilon}G[f(x)+\varepsilon h(x)] \right|_{\varepsilon=0}= \left.{\d\over\d\varepsilon}(f(x)+\varepsilon h(x)) \right|_{\varepsilon=0}= h(x)](../../_images/math/7dd417d049064080709b9c9c5268279b1530fa30.png)
thus we write 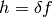 and
and
![\delta F[f]=\int {\delta F\over\delta f(x)}\delta f(x)\d x](../../_images/math/fa073632306ec146fbbaab3afd4d93610653f6e3.png)
so 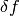 have two meanings — it’s either
have two meanings — it’s either
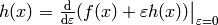 (a finite change in the function
(a finite change in the function 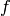 ) or a variation
of a functional, depending on the context. Some mathematicians don’t like to
write
) or a variation
of a functional, depending on the context. Some mathematicians don’t like to
write 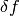 in the meaning of
in the meaning of 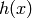 , they prefer to write the latter, but
it is in fact perfectly fine to use
, they prefer to write the latter, but
it is in fact perfectly fine to use 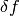 , because it is completely analogous to
, because it is completely analogous to 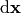 .
.
The correspondence between the finite and infinite dimensional case can be summarized as:
![\begin{eqnarray*} f(x_i) \quad&\Longleftrightarrow&\quad F[f] \\ \d f=0 \quad&\Longleftrightarrow&\quad \delta F=0 \\ {\partial f\over\partial x_i}=0 \quad&\Longleftrightarrow&\quad {\delta F\over\delta f(x)}=0 \\ f \quad&\Longleftrightarrow&\quad F \\ x_i \quad&\Longleftrightarrow&\quad f(x) \\ x \quad&\Longleftrightarrow&\quad f \\ i \quad&\Longleftrightarrow&\quad x \\ \end{eqnarray*}](../../_images/math/847f04226ae2cb7a6dd56aee63bc4e3292504c66.png)
More generally, 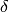 -variation can by applied to any function
-variation can by applied to any function 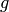 which contains the function
which contains the function 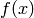 being varied, you just need to replace
being varied, you just need to replace 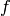 by
by 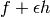 and apply
and apply 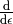 to the whole
to the whole 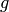 , for example (here
, for example (here 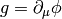 and
and 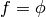 ):
):
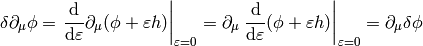
This notation allows us a very convinient computation, as shown in the following examples. First, when computing a variation of some integral, when can interchange 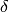 and
and 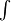 :
:
![F[f]=\int K(x) f(x) \d x](../../_images/math/90c6e5cb0f8047f52f0362c62ae0b152748eab17.png)
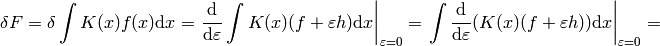
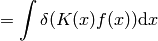
In the expression 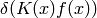 we must understand from the context if we are treating it as a functional of
we must understand from the context if we are treating it as a functional of 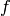 or
or 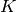 . In our case it’s a functional of
. In our case it’s a functional of 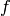 , so we have
, so we have 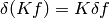 .
.
A few more examples:
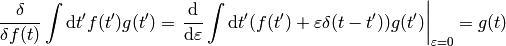
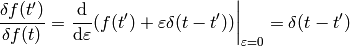
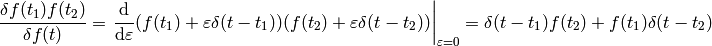
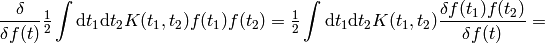
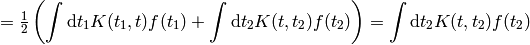
The last equality follows from 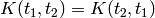 (any antisymmetrical part of a
(any antisymmetrical part of a 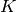 would not contribute to the symmetrical integration).
would not contribute to the symmetrical integration).
Another example is the derivation of Euler-Lagrange equations for the
Lagrangian density 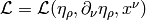 :
:
![0 = \delta I = \delta \int \L \,\d^4x^\mu
= \int \partial \L \,\d^4x^\mu
= \int { \partial \L\over\partial \eta_\rho}\delta\eta_\rho
+
{ \partial \L\over\partial (\partial_\nu \eta_\rho)}
\delta(\partial_\nu\eta_\rho)
\,\d^4x^\mu
=
= \int { \partial \L\over\partial \eta_\rho}\delta\eta_\rho
+
{ \partial \L\over\partial (\partial_\nu \eta_\rho)}
\partial_\nu(\delta\eta_\rho)
\,\d^4x^\mu
=
= \int { \partial \L\over\partial \eta_\rho}\delta\eta_\rho
-
\partial_\nu\left(
{ \partial \L\over\partial (\partial_\nu \eta_\rho)}
\right)
\delta\eta_\rho
\,\d^4x^\mu
+\int \partial_\nu \left(
{ \partial \L\over\partial (\partial_\nu \eta_\rho)}
\delta\eta_\rho
\right)
\,\d^4x^\mu
=
= \int \left[{ \partial \L\over\partial \eta_\rho}
-
\partial_\nu\left(
{ \partial \L\over\partial (\partial_\nu \eta_\rho)}
\right)
\right]
\delta\eta_\rho
\,\d^4x^\mu](../../_images/math/ca3df7ea8ec0fdf676a58b601e6200e37f07ab31.png)
Another example:
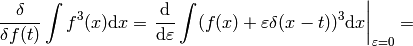
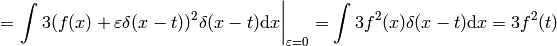
Some mathematicians would say the above calculation is incorrect, because
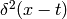 is undefined. But that’s not exactly true, because in case of
such problems the above notation automatically implies working with some
sequence
is undefined. But that’s not exactly true, because in case of
such problems the above notation automatically implies working with some
sequence 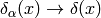 (for example
(for example 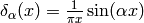 ) and taking the limit
) and taking the limit 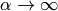 :
:
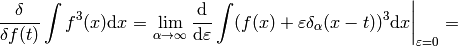
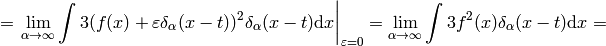
(6)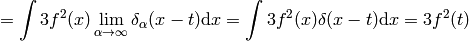
As you can see, we got the same result, with the same rigor, but using an obfuscating notation. That’s why such obvious manipulations with 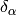 are tacitly implied.
are tacitly implied.
Spherical Harmonics¶
Are defined by
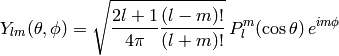
where 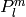 are associated Legendre polynomials defined by
are associated Legendre polynomials defined by
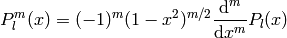
and 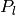 are Legendre polynomials defined by the formula
are Legendre polynomials defined by the formula
![P_l(x)={1\over2^l l!}{\d^l\over\d x^l}[(x^2-1)^l]](../../_images/math/9d4375f23c92f4a73c90f97bbc1430f727daae3a.png)
they also obey the completeness relation
(7)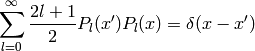
The spherical harmonics are ortonormal:
(8)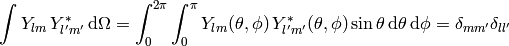
and complete (both in the 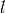 -subspace and the whole space):
-subspace and the whole space):
(9)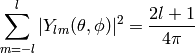
(10)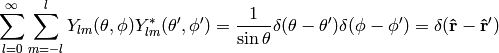
The relation (9) is a special case of an addition theorem for spherical harmonics
(11)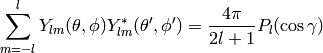
where 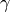 is the angle between the unit vectors given by
is the angle between the unit vectors given by 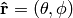 and
and 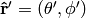 :
:
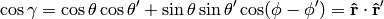
Dirac Notation¶
The Dirac notation allows a very compact and powerful way of writing equations that describe a function expansion into a basis, both discrete (e.g. a fourier series expansion) and continuous (e.g. a fourier transform) and related things. The notation is designed so that it is very easy to remember and it just guides you to write the correct equation.
Let’s have a function 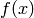 . We define
. We define
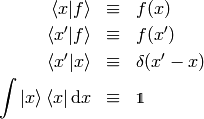
The following equation
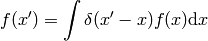
then becomes
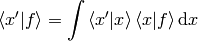
and thus we can interpret 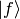 as a vector,
as a vector, 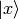 as a basis and
as a basis and 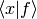 as the coefficients in the basis expansion:
as the coefficients in the basis expansion:
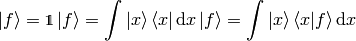
That’s all there is to it. Take the above rules as the operational definition
of the Dirac notation. It’s like with the delta function - written alone it
doesn’t have any meaning, but there are clear and non-ambiguous rules to
convert any expression with 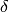 to an expression which even mathematicians
understand (i.e. integrating, applying test functions and using other relations
to get rid of all
to an expression which even mathematicians
understand (i.e. integrating, applying test functions and using other relations
to get rid of all 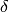 symbols in the expression – but the result is
usually much more complicated than the original formula). It’s the same with
the ket
symbols in the expression – but the result is
usually much more complicated than the original formula). It’s the same with
the ket 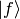 : written alone it doesn’t have any meaning, but you can
always use the above rules to get an expression that make sense to everyone
(i.e. attaching any bra to the left and rewriting all brackets
: written alone it doesn’t have any meaning, but you can
always use the above rules to get an expression that make sense to everyone
(i.e. attaching any bra to the left and rewriting all brackets 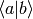 with their equivalent expressions) – but it will be more complex and harder to
remember and – that is important – less general.
with their equivalent expressions) – but it will be more complex and harder to
remember and – that is important – less general.
Now, let’s look at the spherical harmonics:
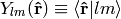
on the unit sphere, we have
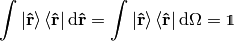
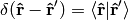
thus
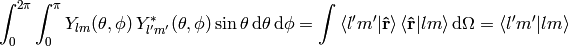
and from (8) we get
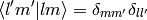
now
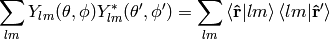
from (10) we get
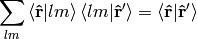
so we have
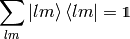
so 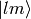 forms an orthonormal basis. Any function defined on the sphere
forms an orthonormal basis. Any function defined on the sphere 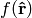 can be written using this basis:
can be written using this basis:
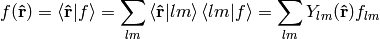
where
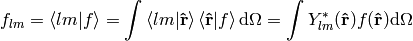
If we have a function 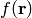 in 3D, we can write it as a function of
in 3D, we can write it as a function of 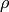 and
and 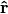 and expand only with respect to the variable
and expand only with respect to the variable 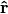 :
:
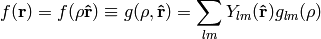
In Dirac notation we are doing the following: we decompose the space into the angular and radial part
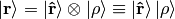
and write
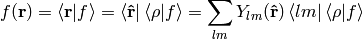
where
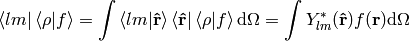
Let’s calculate 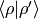
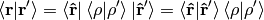
so
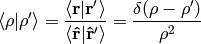
We must stress that  only acts in the
only acts in the 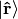 space (not the
space (not the 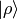 space) which means that
space) which means that
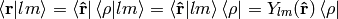
and 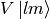 leaves
leaves 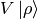 intact. Similarly,
intact. Similarly,
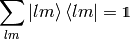
is a unity in the 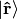 space only (i.e. on the unit sphere).
space only (i.e. on the unit sphere).
Let’s rewrite the equation (11):
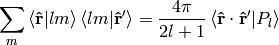
Using the completeness relation (7):
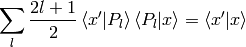
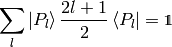
we can now derive a very important formula true for every function 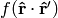 :
:
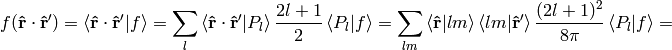
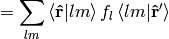
where
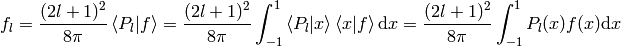
or written explicitly
(12)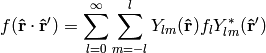
Homogeneous functions¶
A function of several variables 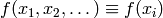 is
homogeneous of degree
is
homogeneous of degree 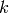 if
if
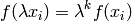
By differentiating with respect to 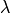 :
:
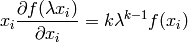
and setting 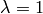 we get the so called Euler equation:
we get the so called Euler equation:
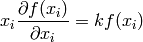
in 3D this can also be written as:
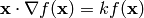
Example¶
The function 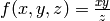 is homogeneous of degree 1, because:
is homogeneous of degree 1, because:
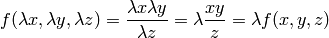
and the Euler equation is:
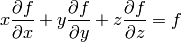
or
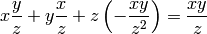
Which obviously is true.