MHD Equations¶
Introduction¶
The magnetohydrodynamics (MHD) equations are:
(1)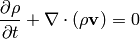
(2)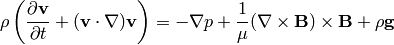
(3)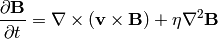
(4)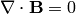
assuming 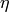 is constant. See the next section for a derivation. We can now
apply the following identities (we use the fact that
is constant. See the next section for a derivation. We can now
apply the following identities (we use the fact that 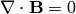 ):
):
![\left[(\nabla\times{\bf B}) \times {\bf B}\right]_i =
\varepsilon_{ijk}(\nabla\times{\bf B})_j B_k =
\varepsilon_{ijk}\varepsilon_{jlm}(\partial_l B_m)B_k =
(\delta_{kl}\delta_{im}-\delta_{km}\delta_{il})(\partial_l B_m)B_k =
=(\partial_k B_i)B_k - (\partial_i B_k)B_k
=\left[({\bf B}\cdot\nabla){\bf B} -
{1\over2}\nabla|{\bf B}|^2\right]_i
(\nabla\times{\bf B}) \times {\bf B} &=
({\bf B}\cdot\nabla){\bf B} - {1\over2}\nabla|{\bf B}|^2=
({\bf B}\cdot\nabla){\bf B} + {\bf B}(\nabla\cdot{\bf B})
- {1\over2}\nabla|{\bf B}|^2
=\nabla\cdot({\bf B}{\bf B}^T) - {1\over2}\nabla|{\bf B}|^2\\
\nabla\times({\bf v} \times {\bf B}) &=
({\bf B}\cdot\nabla){\bf v} - {\bf B}(\nabla\cdot{\bf v})
+{\bf v}(\nabla\cdot {\bf B}) - ({\bf v}\cdot\nabla) {\bf B}
=
\nabla\cdot({\bf B}{\bf v}^T - {\bf v}{\bf B}^T)\\
\nabla\cdot(\rho{\bf v}{\bf v}^T) &=
\left(\nabla\cdot(\rho{\bf v})\right){\bf v}
+ \rho({\bf v}\cdot\nabla){\bf v}=
-{\bf v}\frac{\partial \rho}{\partial t}
+ \rho({\bf v}\cdot\nabla){\bf v}](../../_images/math/16cce62f3e1051af600aee5e8570ed1b52bd6f60.png)
So the MHD equations can alternatively be written as:
(5)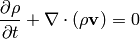
(6)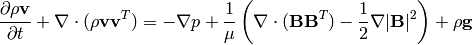
(7)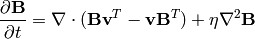
(8)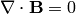
One can also introduce a new variable 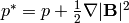 , that simplifies (6) a bit.
, that simplifies (6) a bit.
Derivation¶
The above equations can easily be derived. We have the continuity equation:
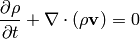
Navier-Stokes equations (momentum equation) with the Lorentz force on the right-hand side:
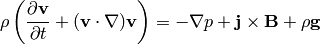
where the current density 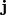 is given by the Maxwell equation (we
neglect the displacement current
is given by the Maxwell equation (we
neglect the displacement current 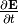 ):
):
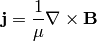
and the Lorentz force:
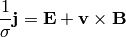
from which we eliminate 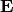 :
:
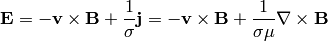
and put it into the Maxwell equation:
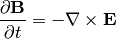
so we get:
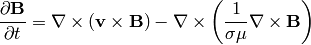
assuming the magnetic diffusivity 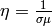 is constant, we
get:
is constant, we
get:
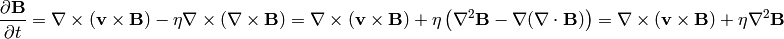
where we used the Maxwell equation:
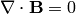
Finite Element Formulation¶
We solve the following ideal MHD equations (we use
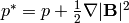 , but we drop the star):
, but we drop the star):
(9)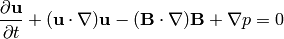
(10)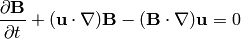
(11)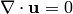
(12)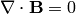
If the equation (12) is satisfied initially, then it is
satisfied all the time, as can be easily proved by applying a divergence to
the Maxwell equation
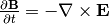 (or the
equation (10), resp. (3)) and we get
(or the
equation (10), resp. (3)) and we get
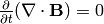 , so
, so
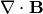 is constant, independent of time. As a consequence,
we are essentially only solving equations (9), (10) and
(11), which consist of 5 equations for 5 unknowns
(components of
is constant, independent of time. As a consequence,
we are essentially only solving equations (9), (10) and
(11), which consist of 5 equations for 5 unknowns
(components of 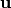 ,
, 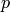 and
and 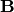 ).
).
We discretize in time by introducing a small time step 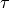 and we also
linearize the convective terms:
and we also
linearize the convective terms:
(13)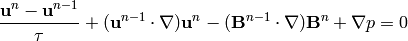
(14)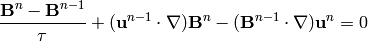
(15)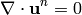
Testing (13) by the test functions 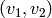 , (14) by
the functions
, (14) by
the functions 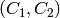 and (15) by the test function
and (15) by the test function
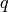 , we obtain the following weak formulation:
, we obtain the following weak formulation:
(16)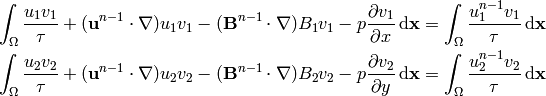
(17)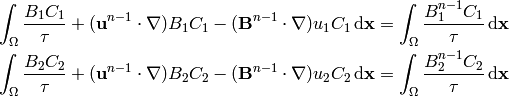
(18)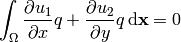
To better understand the structure of these equations, we write it using bilinear and linear forms, as well as take into account the symmetries of the forms. Then we get a particularly simple structure:
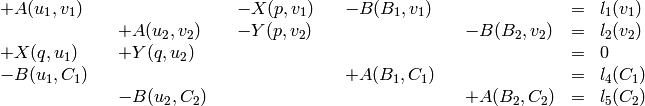
where:
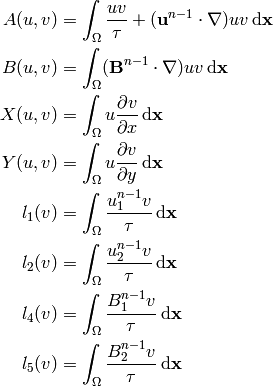
E.g. there are only 4 distinct bilinear forms. Schematically we can visualize the structure by:
| A | -X | -B | ||
| A | -Y | -B | ||
| X | Y | |||
| -B | A | |||
| -B | A |
In order to solve it with Hermes, we first need to write it in the block form:
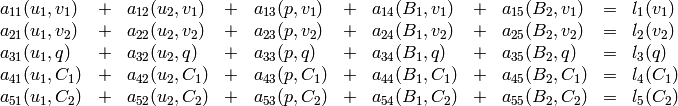
comparing to the above, we get the following nonzero forms:
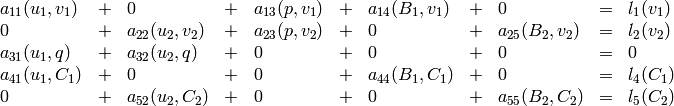
where:
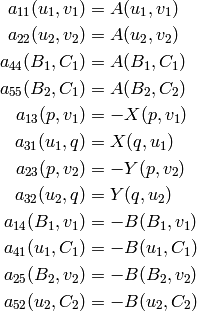
and  , ...,
, ...,  are the same as above.
are the same as above.