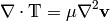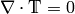Fluid Dynamics¶
Stress-Energy Tensor¶
In general, the stress energy tensor is the flux of momentum  over the
surface
over the
surface  . It is a machine that contains a knowledge of the energy
density, momentum density and stress as measured by any observer of the event.
. It is a machine that contains a knowledge of the energy
density, momentum density and stress as measured by any observer of the event.
Imagine a (small) box in the spacetime. Then the observer with a 4-velocity
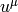 measures the density of 4-momentum
measures the density of 4-momentum 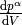 in his frame as:
in his frame as:
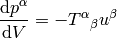
and the energy density that he measures is:
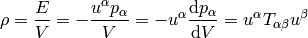
One can also obtain the stress energy tensor from the Lagrangian
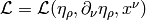 by combining the
Euler-Lagrange equations
by combining the
Euler-Lagrange equations
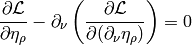
with the total derivative 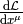 :
:
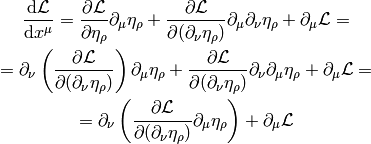
or
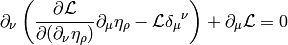
This can be written as:
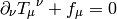
where
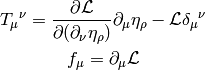
The Navier-Stokes equations can be derived from the conservation law:
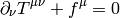
To obtain some Lagrangian (and action) for the perfect fluid, so that we can
derive the stress energy tensor 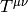 from that, is not trivial, see for
example arXiv:gr-qc/9304026. One has to
take into account the equation of state and incorporate the particle number
conservation
from that, is not trivial, see for
example arXiv:gr-qc/9304026. One has to
take into account the equation of state and incorporate the particle number
conservation 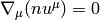 and no entropy exchange
and no entropy exchange
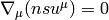 constraints.
constraints.
The equation of continuity follows from the
conservation of the baryon number — the volume 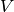 that contains certain
number of baryons can change, but the total number of baryons
that contains certain
number of baryons can change, but the total number of baryons 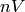 must remain
constant:
must remain
constant:
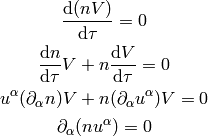
Perfect Fluids¶
Perfect fluids have no heat conduction (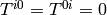 ) and no
viscosity (
) and no
viscosity (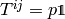 ), so in the comoving frame:
), so in the comoving frame:
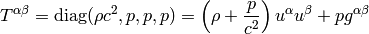
where in the comoving frame we have 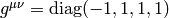 ,
, 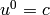 and
and 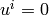 ,
but
,
but 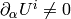 .
. 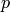 is the pressure with units
is the pressure with units
![[p] =\rm N\,m^{-2}=kg\,m^{-1}\,s^{-2}](../../_images/math/38538eb1bee3ecd3de4b08d6fdf7e28585065ceb.png) (then
(then
![[{p\over c^2}] =\rm kg\,m^{-3}](../../_images/math/425bf23372113448c8ac1d14f2baabb8a740fe88.png) ),
), 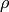 is the rest mass density with units
is the rest mass density with units
![[\rho] =\rm kg\,m^{-3}](../../_images/math/bd6ffca970962deb42030ae9049645062780249f.png) , and
, and 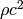 is the energy density with units
is the energy density with units
![[\rho c^2] =\rm kg\,m^{-1}\,s^{-2}](../../_images/math/900a45e031d50d973868ee812a015c84cc4bb3ae.png) .
.
The last equation is a tensor equation so it holds in any frame. Let’s write the components explicitly:
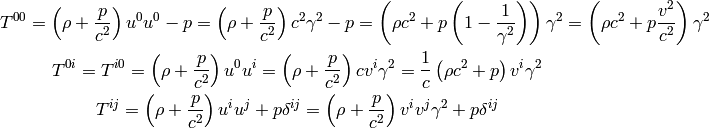
We now use the conservation of the stress energy tensor and the conservation of the number of particles:
(1)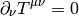
(2)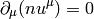
The equation (2) gives:
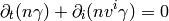
(3)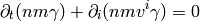
(4)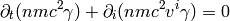
The equation (1) gives for 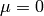 :
:
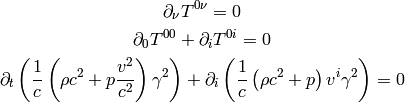
(5)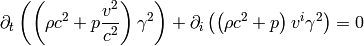
We now substract the equation (4) from (5):
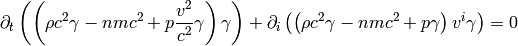
We define the nonrelativistic energy as:
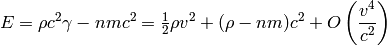
so it contains the kinetic plus internal energies. We substitute back into (5):
(6)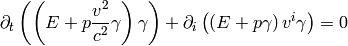
This is the relativistic equation for the energy. Substituting
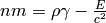 into
(3):
into
(3):
(7)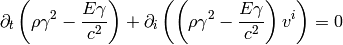
For 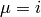 we get:
we get:
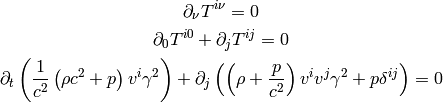
(8)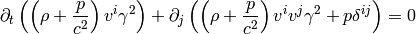
This is the momentum equation. The equations (7), (8) and (6) are the correct relativistic equations for the perfect fluid (no approximations were done). We can take either (7) or (5) as the equation of continuity (both give the same nonrelativistic equation of continuity). Their Newtonian limit is:
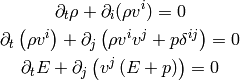
those are the Euler equations, also sometimes written as:
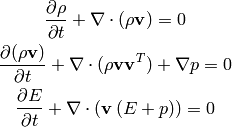
Energy Equation¶
The energy equation can also be derived from thermodynamic and the other two Euler equations. We have the following two Euler equations:
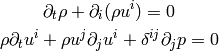
We’ll need the following formulas:
![\partial_t (u_i u^i) = (\partial_t u_i) u^i + u_i \partial_t u^i =
(\partial_t u_i)\delta^{ij} u_j + u_i \partial_t u^i =
= (\partial_t u_i\delta^{ij}) u_j + u_i \partial_t u^i =
(\partial_t u^j) u_j + u_i \partial_t u^i =
2 u_i \partial_t u^i
\partial_j (u_i u^i) = 2 u_i \partial_j u^i
\partial_t\rho =- \partial_i(\rho u^i)
\partial_t u^i =- u^j\partial_j u^i - {\delta^{ij}\over\rho}\partial_j p
- u^j\partial_j p + \partial_t(\rho U) =
= - {\d p \over\d t} +\partial_t p + \partial_t(\rho U) =
= - {\d p \over\d t} +\partial_t (\rho U + p) =
= - {\d p \over\d t} +{\d\over\d t} (\rho U + p)
-u^j\partial_j (\rho U + p)=
= - {\d p \over\d t} +{\d\rho\over\d t} \left(U + {p\over\rho}\right)
+\rho{\d\over\d t} \left(U + {p\over\rho}\right)
-u^j\partial_j (\rho U + p)=
= - {\d p \over\d t} +{\d\rho\over\d t} \left(U + {p\over\rho}\right)
+\rho{\d\over\d t} \left(U + {p\over\rho}\right)
+ (\rho U + p)\partial_j u^j
-\partial_j (\rho U u^j + p u^j) =
= \left[\rho {\d\over\d t}\left(U + {p\over\rho}\right) - {\d p\over\d t}
\right]
+
\left(U + {p\over\rho}\right)\left[ {\d\rho\over\d t} + \rho
\partial_j u^j \right]
-\partial_j (\rho U u^j + p u^j) =
= - \partial_j(\rho U u^j + p u^j)
0 = \d Q = T\d S = \d U + p\d V = \d (U + pV) - V\d p
= \d\left(U+{p\over\rho}\right) - {1\over \rho}\d p
= \d H - {1\over \rho}\d p](../../_images/math/a91562b898340209ea21caef92fedd6e96c40af1.png)
where 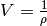 is the specific volume and
is the specific volume and
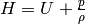 is entalphy (heat content).
is entalphy (heat content).
Then:
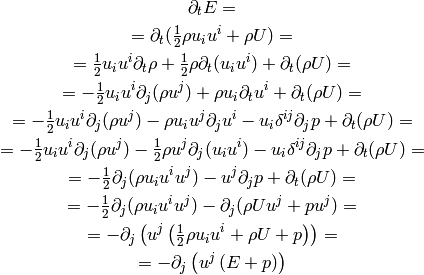
so:
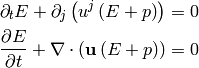
Bernoulli’s Principle¶
Bernoulli’s principle works for a perfect fluid, so we take the Euler equations:
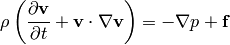
and put it into a vertical gravitational field 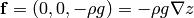 , so:
, so:
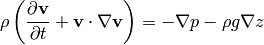
we divide by 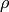 :
:
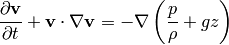
and use the identity 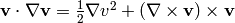 :
:
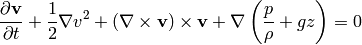
so:
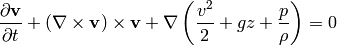
If the fluid is moving, we integrate this along a streamline from the point 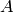 to
to 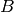 :
:
![\int {\partial {\bf v}\over\partial t} \cdot \d {\bf l} +\left[{v^2\over 2} + gz + {p\over\rho} \right]_A^B=0](../../_images/math/ed384b2c8b9985d9a9b74c872174d0f686c19b7f.png)
So far we didn’t do any approximation (besides having a perfect fluid in a
vertical gravitation field).
Now we assume a steady flow, so 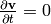 and since points
and since points 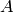 and
and 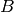 are arbitrary, we get:
are arbitrary, we get:
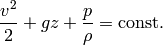
along the streamline. This is called the Bernoulli’s principle.
If the fluid is not moving, we set 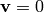 in the equations above and
immediately get:
in the equations above and
immediately get:
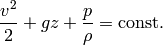
The last equation then holds everywhere in the (nonmoving) fluid (as opposed to the previous equation that only holds along the streamline).
Hydrostatic Pressure¶
Let 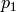 be the pressure on the water surface and
be the pressure on the water surface and 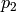 the pressure
the pressure 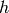 meters below the surface. From the Bernoulli’s principle:
meters below the surface. From the Bernoulli’s principle:
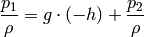
so
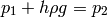
and we can see, that the pressure 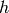 meters below the surface is
meters below the surface is 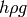 plus the (atmospheric) pressure
plus the (atmospheric) pressure 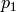 on the surface.
on the surface.
Torricelli’s Law¶
We want to find the speed  of the water flowing out of the tank (of the
height
of the water flowing out of the tank (of the
height 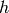 ) through a small hole at the bottom. The (atmospheric) pressure at
the water surface and also near the small hole is
) through a small hole at the bottom. The (atmospheric) pressure at
the water surface and also near the small hole is 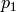 . From the Bernoulli’s
principle:
. From the Bernoulli’s
principle:
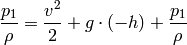
so:
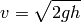
This is called the Torricelli’s law.
Venturi Effect¶
A pipe with a cross section 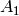 , pressure
, pressure 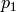 and the speed of a
perfect liquid
and the speed of a
perfect liquid 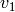 changes it’s cross section to
changes it’s cross section to 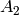 , so the pressure
changes to
, so the pressure
changes to 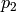 and the speed to
and the speed to 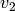 . Given
. Given 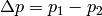 ,
, 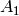 and
and
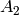 , calculate
, calculate 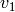 and
and 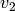 .
.
We use the continuity equation:
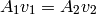
and the Bernoulli’s principle:
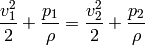
so we have two equations for two unknowns 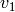 and
and 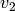 , after solving it we
get:
, after solving it we
get:
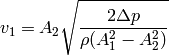
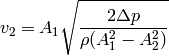
Hagen-Poiseuille Law¶
We assume incompressible (but viscuous) Newtonean fluid (in no external force field):
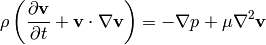
flowing in the vertical pipe of radius 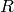 and we further assume steady flow
and we further assume steady flow
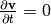 , axis symmetry
, axis symmetry
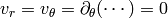 and a fully developed flow
and a fully developed flow 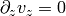 . We write the Navier-Stokes equations above in the cylindrical
coordinates and using the stated assumptions, the only nonzero equations are:
. We write the Navier-Stokes equations above in the cylindrical
coordinates and using the stated assumptions, the only nonzero equations are:
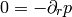
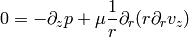
from the first one we can see the 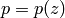 is a function of
is a function of  only and we can
solve the second one for
only and we can
solve the second one for 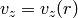 :
:
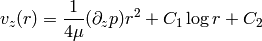
We want 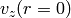 to be finite, so
to be finite, so 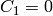 , next we assume the no slip
boundary conditions
, next we assume the no slip
boundary conditions 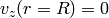 , so
, so 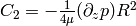 and we get the parabolic velocity profile:
and we get the parabolic velocity profile:
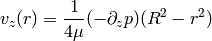
Assuming that the pressure decreases linearly across the length of the pipe, we
have 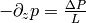 and we get:
and we get:
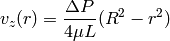
We can now calculate the volumetric flow rate:
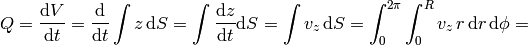
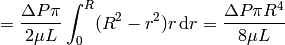
so we can see that it depends on the 4th power of 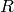 . This is called the
Hagen-Poiseuille law.
. This is called the
Hagen-Poiseuille law.
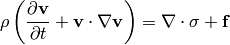
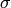 can be written as:
can be written as: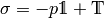
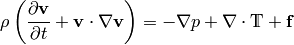
 to be isotropic, linear in strain
rates and it’s divergence zero for fluid at rest. It follows that the only way
to write the tensor under these conditions is:
to be isotropic, linear in strain
rates and it’s divergence zero for fluid at rest. It follows that the only way
to write the tensor under these conditions is: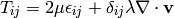
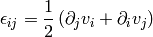
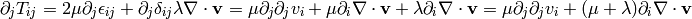
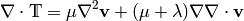
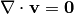 , so we get the
incompressible Navier-Stokes equations:
, so we get the
incompressible Navier-Stokes equations: