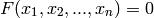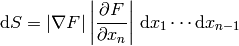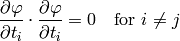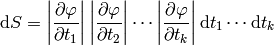Integration¶
This chapter doesn’t assume any knowledge about differential geometry. The most versatile way to do integration over manifolds is explained in the differential geometry section.
General Case¶
We want to integrate a function 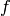 over a
over a 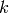 -manifold in
-manifold in 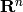 , parametrized
as:
, parametrized
as:
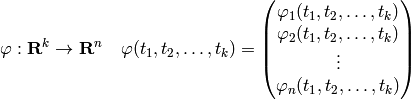
then the integral of 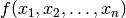 over
over 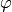 is:
is:
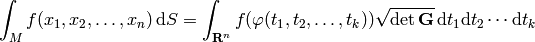
where 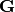 is called a Gram matrix and
is called a Gram matrix and 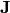 is a Jacobian:
is a Jacobian:
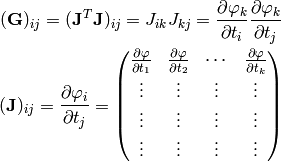
The idea behind this comes from the fact that the volume of the 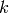 -dimensional
parallelepiped spanned by the vectors
-dimensional
parallelepiped spanned by the vectors
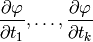
is given by
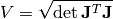
where 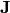 is an
is an 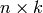 matrix having those vectors as its column
vectors.
matrix having those vectors as its column
vectors.
Example¶
Let’s integrate a function 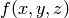 over the surface of a sphere in 3D
(e.g.
over the surface of a sphere in 3D
(e.g. 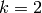 and
and 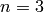 ):
):
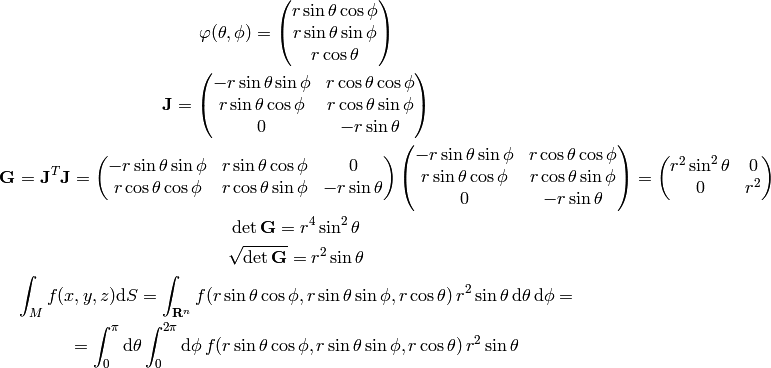
Let’s say we want to calculate the surface area of a sphere, so we set 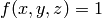 and get:
and get:
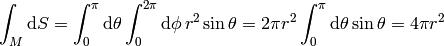
Special Cases¶
k = n¶
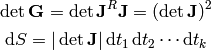
k = 1¶
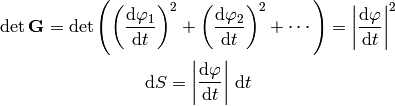
k = n - 1¶
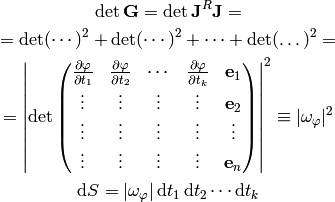
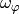 is a generalization of a vector cross product. The
is a generalization of a vector cross product. The
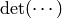 symbol means a determinant of a matrix with one row removed
(first term in the sum has first row removed, second term has second row
removed, etc.).
symbol means a determinant of a matrix with one row removed
(first term in the sum has first row removed, second term has second row
removed, etc.).
k = 2, n = 3¶
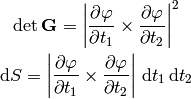
Motivation¶
Let the 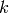 -dimensional parallelepiped P be spanned by the vectors
-dimensional parallelepiped P be spanned by the vectors
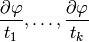
and let 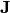 is
is 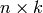 matrix having these vectors as its column
vectors. Then the area of P is
matrix having these vectors as its column
vectors. Then the area of P is
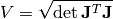
so the definition of the integral over a manifold is just approximating the surface by infinitesimal parallelepipeds and integrating over them.
Example¶
Let’s calculate the total distance traveled by a body in 1D, whose position is
given by 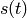 :
:
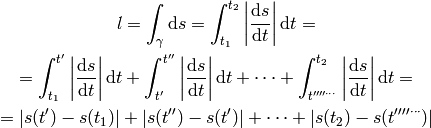
where 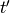 ,
, 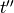 , ... are all the points at which
, ... are all the points at which 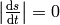 , so each of the integrals in the above sum has either positive or
negative integrand.
, so each of the integrals in the above sum has either positive or
negative integrand.
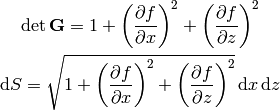
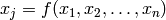 we get:
we get: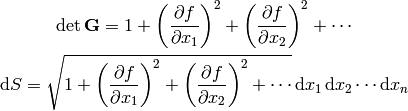
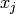 ” term is missing in the sums above.
” term is missing in the sums above.